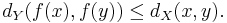Metric map

In the mathematical theory of metric spaces, a metric map is a function between metric spaces that does not increase any distance (such functions are always continuous). These maps are the morphisms in the category of metric spaces, Met (Isbell 1964). They are also called Lipschitz functions with Lipschitz constant 1, nonexpansive maps, nonexpanding maps, weak contractions, or short maps.

Specifically, suppose that X and Y are metric spaces and ƒ is a function from X to Y. Then we have a metric map when, for any points x and y in X,

d_{Y}(f(x),f(y)) \leq d_{X}(x,y) . \!

Here dX and dY denote the metrics on X and Y respectively.

A map ƒ between metric spaces is an isometry if and only if 1) it is metric, 2) it is a bijection, and 3) its inverse is also metric. The composite of metric maps is also metric. Thus metric spaces and metric maps form a category Met; Met is a subcategory of the category of metric spaces and Lipschitz functions, and the isomorphisms in Met are the isometries.

One can say that ƒ is strictly metric if the inequality is strict for every two different points. Then a contraction mapping is strictly metric, but not necessarily the other way around. Note that an isometry is never strictly metric, except in the degenerate case of the empty space or a single-point space.

References